Масштабирование, системы координат. Опции

[za-ek]

Здравствуйте!
Пишу графическое приложение на Qt 4.6, замучался с перемещением центра.. Имеется QGraphicsScene и QGraphicsView.
Задача.
При приближении и отдалении сцены необходимо, что бы под мышкой остались те же координаты, т.е., пример :
Центр сцены расположен в точке {0;0}, мышь находится в точке {-20;-20} (в системе координат сцены), теперь функцией QGraphicsView::scale(scaleFactor,scaleFactor) приближаю сцену, центр остаётся на месте, следовательно, точка под мышью съезжает, она станет {-16,-16}, есть три системы координат:
1. QGraphicsScene (x вправо, y вниз, центр посередине)
2. QGraphicsView (x вправо, y вниз, центр в верхнем левом углу)
3. Система координат центра сцены (x влево, y вверх)

Я перепробовал уже тучу вариантов, по идее, должно быть так :
Центр должен быть смещён на величину смещения мыши относительно 3й системы координат + смещение центра 1й системы координат, умноженное на scaleFactor.
Но в этом случае центр улетает совсем не туда куда надо, помогите, пожалуйста, в математике вроде не дуб, но не выходит совсем..

[Алексей1153]

тоже как-то бился над похожей задачей, но не в Qt

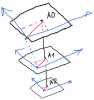
чисто алгоритмически решение следующее:

пусть точка А0 (на экране) - это проекция точки А1 сцены с масштабом М1. После применения масштаба М2 проекция точки А2 сцены должна остаться на том же месте. Если представить все три поверхности на расстоянии (а мы как бы сверху смотрим на точку А0 , совпадающую с А1 и А2) , то получается такой пирог:



линия А0-А1-А2 является прямой, перпендикулярной всем трём поверхностям

ключевой момент - работа с вектором, показанным красным сплошным цветом. Синим показаны оси системы координат - именно они будут "отъезжать"

И ещё одна грабля: когда, к примеру, колесом меняют масштаб, коэффициент масштабирования (раз/оборот колеса) нужно линейно менять. Если он будет постоянным, то масштабирование будет производиться с ускорением, а не быть равномерным

Сообщение отредактировал Алексей1153 - 13.7.2012, 16:12