пример посмотрел, компилить - компилится. что дальше делать - не пойму. нужно достроить граф, чтобы обеспечить двусвязность.
 РЈРСВВВВВВВВВеньшено Р В Р’В Р СћРІР‚ВВВВВВВВР С• 16% 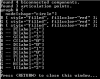
313 x 246 (7.17 килобайт)
|
как можно использовать эту информацию? понятно, что эти articulations points нужно с чем-нибудь соединить, но как, чтобы по-хорошему всё было? покороче и покрасивше. у меня граф взвешенный, кстати, в отличие от примера
Сообщение отредактировал efg - 27.3.2012, 22:09


 27.3.2012, 22:01
27.3.2012, 22:01


 0
0 
 28.3.2012, 8:54
28.3.2012, 8:54






 12
12 
 3.6.2012, 4:52
3.6.2012, 4:52


 0
0 









 РЈРСВВВВВВВВВеньшено Р В Р’В Р СћРІР‚ВВВВВВВВР С• 16%
РЈРСВВВВВВВВВеньшено Р В Р’В Р СћРІР‚ВВВВВВВВР С• 16%



